摘 要
随着计算机网络和信息技术的发展,信息安全在各领域发挥着越来越重要的作用,其中密码学已成为信息安全技术的核心,本文主要介绍了信息加密技术的应用。
RSA算法是目前公认的在理论和实际应用中最为成熟和完善的一种公钥密码体制,它是第一个既能用于数据加密也能用于数字签名的算法,是公钥密码体制的代表。数字签名是起到身份认证、核准数据完整性的一种信息安全技术。它通过认证技术来辨认真伪。RSA数字签名体制使用的是RSA公开密钥密码算法进行数字签名。
本文主要研究的内容包括:第一,对RSA算法进行了全面系统的介绍,包括RSA算法的应用现状和原理—大素数的产生、密钥对的产生、对明文的加密运算和密文的解密运算,为具体实现打下了理论基础;第二,介绍了RSA数字签名的一些基本概念和数字签名的理论实现过程;第三,对MD5算法基本原理的介绍;第四,详述了RSA数字签名的设计与实现,主要实现的模块包括RSA密钥的产生(一对公钥和私钥),RSA加密算法和解密算法的实现,消息摘要MD的生成以及利用RSA算法实现数字签名和签名的验证;第五,对该系统进行了整体的测试和分析改进;第六,分析了RSA数字签名的安全性,指出了RSA数字签名的发展方向。
关键字:RSA算法;加密; 解密;MD5算法;RSA数字签名
The Design and Realization of Digital Signature Based on RSA
Abstract
With the development of the computer network and information technology, information security plays more and more important role in every field. Cryptography has become the core of information security technology. This thesis mainly introduces the application of information encryption technology.
RSA algorithm is considered as a public-key cryptosystem of the most fully developed and complete in theory and practice application at present. It is the first algorithm for both data encryption and digital signature. Digital signature is an information security technology used to check authentication and data integrity. It identifies true or false by the authentication technology. RSA digital signature system carries on digital signature by using RSA public-key cipher algorithm.
The main content of this thesis includes six parts. First of all, it is a comprehensive systematic introduction about RSA algorithm including the present application situation and principle of RSA algorithm----producing big prime numbers and secret keys, the encryption arithmetic for information and the decryption for secret information, which establish the theory foundation for achieving concrete; secondly, it introduces some basic conception of RSA digital signature and theory of digital signature realizing process; thirdly, it introduces the basic principle of MD5 algorithm; fourthly, it states design and realization of RSA digital signature in detail. The main modules includes producing RSA secret keys (a public key and private key ), implementation of RSA encryption algorithm and decryption algorithm, producing message digest and realizing digital signature and verification by RSA; the fifth, it carries on testing entirely, analyzing and improving for this system;The sixth, it analyses the security of RSA digital signature and points out the development direction of RSA digital signature.
Key words: RSA algorithm; encryption; decryption; MD5 algorithm; RSA digital signature
2 RSA算法和RSA数字签名算法的基本概念和原理
2.1 RSA算法的基本概念和原理
2.1.1 RSA算法介绍与应用现状
RSA算法是一种公钥密码算法,实现RSA算法包括生成RSA密钥,加密和解密数据。RSA算法是第一个能同时用于加密和数字签名的算法,也易于理解和操作。RSA是被研究得最广泛的公钥算法,从提出到现在已近二十年,经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何,而且密码学界多数人士倾向于因子分解不是NP-C问题。RSA的缺点主要有:A)产生密钥很麻烦,受到素数产生技术的限制,因而难以做到一次一密。B)分组长度太大,为保证安全性,n 至少也要 600 bits。
RSA算法的时间复杂性取决于它所设计的几个基本运算的时间复杂性。密钥生成过程时间主要是生成随机素数的时间及计算公钥和私钥的模乘法的时间。生成随机素数的时间在于完成对随机大数的Fermat测试的时间,Fermat测试的时间复杂度为O((log2n)3),n所测试的整数。模乘法的计算方法采取先计算两个数的乘积,再取模n,时间复杂性为O((log2n)2)。 RSA加密解密计算的时间主要是模幂运算的时间,即形式为xc mod n的函数的运算时间。模幂算法采取平方乘算法,设l是c的长度,则计算xc mod n至多需要2l次模乘法,因为 1[log2n]+1,所以模幂运算能在时间O((log2n)3)内完成。因此,RSA的加密和解密均可在多项式时间内完成。
RSA公开密钥加密算法自20世纪70年代提出以来,已经得到了广泛认可和应用。发展至今,电子安全领域的各方面已经形成了较为完备的国际规范。RSA作为最重要的公开密钥算法,在各领域的应用数不胜数。RSA在硬件方面,以技术成熟的IC应用于各种消费类电子产品。RSA在软件方面的应用,主要集中在Internet上、加密连接、数字签名和数字证书的核心算法广泛使用RSA。
2.1.2 RSA算法的实现原理
1) 随机选择两个不同的素数p和q,它们的宽度是密钥宽度的二分之一。
2) 计算出p和q的乘积n 。
3) 在2和Φ(n)之间随机选择一个数e , e 必须和Φ(n)互素,整数e用做加密密钥(其中Φ(n)=(p-1)*(q-1))。
4) 从公式ed ≡ 1 mod Φ(n)中求出解密密钥d 。
5) 得公钥(e ,n ), 私钥 (d , n) 。
6) 公开公钥,但不公开私钥。
7) 将明文P (假设P是一个小于n的整数)加密为密文C,计算方法为:
C = P^e mod n;
8) 将密文C解密为明文P,计算方法为:
P=C^d mod n;
然而只根据n和e(不是p和q)要计算出d是不可能的。因此,任何人都可对明文进行加密,但只有授权用户(知道d)才可对密文解密。
2.2 RSA数字签名基本概念和RSA数字签名算法的实现原理
2.2.1 RSA数字签名基本概念
RSA数字签名体制使用了RSA公开密钥密码算法进行数字签名,鉴于RSA算法在实践中已经被证明了的安全性,RSA数字签名体制在许多安全标准中得以广泛应用。ISO/IEC 9796和ANSI X9.30-199X 以及美国联邦信息处理标准FIPS 186-2已经将RSA作为推荐的数字签名标准算法之一。
RSA数字签名算法,包括签名算法和验证签名算法。它是利用的RSA算法的加密和解密算法的原理进行的一种数字签名,实际上是通过一个哈希函数来实现的(本设计是通过的MD5算法)产生消息摘要MD来实现的所需加密的对象。
数字签名的特点是它代表了消息的特征,消息如果发生改变,数字签名的值也将发生改变,不同的消息将得到不同的数字签名。安全的数字签名使接收方可以得到保证:消息确实来自发送方。因为签名的私钥只有发送方自己保存,他人无法做一样的数字签名,如果第三方冒充发送方发出一个消息,而接收方在对数字签名进行解密时使用的是发送方的公开密钥,只要第三方不知道发送方的私有密钥,加密出来的数字签名和经过计算的数字签名必然是不相同的,这就提供了一个安全的确认发送方身份的方法,即数字签名的真实性得到了保证。
数字签名通过认证技术来辨认真伪。认证技术主要包括数字签名认证、身份认证以及公开密钥证明等。数字签名认证机制提供了一种对数字签名进行鉴别的方法;身份认证机制提供了辨别和确认通信双方真实身份的方法;公开密钥证明机制则对密钥进行验证。网络时代中,人们验证数字签名来确定你正在和谁打交道,验证你的文件是否已被黑客篡改。数据的安全性和真实性已成为网络安全中至关重要的一部分。
数字签名类似手书签名,它具有以下的性质:
1)能够验证签名产生者的身份,以及产生签名的日期和时间;
2)能用于证实被签消息内容;
3)数字签名可由第三方验证,从而能够解决通信双方的争议。
为了实现数字签名的以上性质,它就应满足下列要求:
1)签名是可信的:任何人都可以验证签名的有效性;
2)签名是不可伪造的:除了合法的签名者外,任何人伪造其签名是困难的;
3)签名是不可复制的:对一个消息的签名不能通过复制变为另一个消息的签名。如果一个消息的签名是从别处复制得到的,则任何人都可以发现消息与签名之间的不一致性,从而可以拒绝签名的消息;
4)签名的消息是不可改变的:经签名的消息不能篡改,一旦签名的消息被篡改,任何人都可以发现消息与签名之间的不一致性;
5)签名是不可抵赖的:签名者事后不能否认自己的签名。可以由第三方或仲裁方来确认双方的信息,以做出仲裁。
为了满足数字签名的这些要求,例如,通信双方在发送消息时,既要防止接收方或其他第三方伪造,又要防止发送方因对自己的不利而否认,也就是说,为了保证数字签名的真实性。
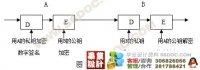
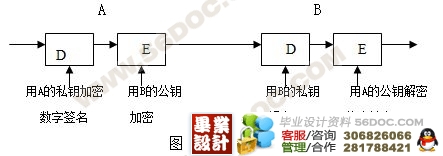
数字签名的原理是:(发送方和接收方根据要求各自产生自己的一对公钥和私钥)
1)被发送文件采用某种算法对原始消息进行运算,得到一个固定长度的数字串,称为消息摘要(MD),不同的消息得到的消息摘要各异,但是对相同的消息它的消息摘要却是唯一的;
2)发送方生成消息的消息摘要,用自己的私钥对摘要进行加密来形成发送方的数字签名;
3)这个数字签名将作为消息的附件和消息一同用接收方的公钥进行加密,将加密后的密文一起发送给接收方;
4)接收方首先把接收到的密文用自己的私钥解密,得到原始消息和数字签名,再用发送方的公钥解密数字签名,随后用同样的算法计算出消息摘要;
5)如果计算出来的消息摘要和发送方发送给他的消息摘要(通过解密数字签名得到的)是相同的,这样接收方就能确认数字签名确实是发送方的,否则就认为收到的消息是伪造的或是中途被篡改的。
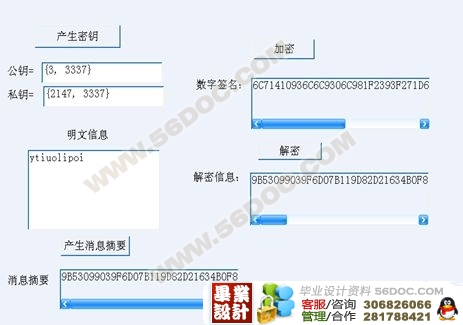
RSA数字签名的运行结果
在本软件中得到二个消息摘要:根据写入的消息(明文信息)计算出来的消息摘要、解密数字签名得到的消息摘要(即是本设计中的解密信息)。如果两个消息摘要是一样的则证明RSA数字签名者的身份的真实性,从而实现了RSA数字签名。该系统的运行结果如图3-5所示。产生的消息摘要和解密得到的消息摘要(在此处是解密信息)是完全一样的,则证明了数字签名的真实性。
目 录
1 引言 1
1.1 研究背景 1
1.2 本课题的研究意义 2
2 RSA算法和RSA数字签名算法的基本概念和原理 2
2.1 RSA算法的基本概念和原理 2
2.1.1 RSA算法介绍与应用现状 2
2.1.2 RSA算法的实现原理 3
2.2 RSA数字签名基本概念和RSA数字签名算法的实现原理 3
2.2.1 RSA数字签名基本概念 3
2.2.2 RSA数字签名算法的实现原理 5
2.3 MD5算法的介绍 6
3 RSA数字签名的设计与实现 7
3.1 RSA数字签名的总体设计 7
3.1.1 RSA数字签名所需实现的功能 7
3.1.2 本软件的总体要求和设计 7
3.2 各部分的设计实现 7
3.2.1 密钥产生的实现 7
3.2.2 产生消息摘要的设计实现 10
3.2.3 数字签名的设计实现 12
3.2.4 验证数字签名的设计与实现 16
3.2.5 RSA数字签名的运行结果 18
4 软件的整体测试和分析改进 18
4.1软件的整体测试 18
4.2 性能分析与改进优化 19
5 RSA数字签名的安全性分析与前景展望 20
5.1 RSA数字签名的安全性分析 20
5.2 RSA数字签名的前景展望 20
结 论 21
参考文献 21
致 谢 22
声 明 23 |